Mathematics A Human Endeavor Answers

I am keeping the following notes from my last session as well.

Harold R. Jacobs (1970) Mathematics: A Human Endeavor

Chapter 1 The Mathematical Way of Thinking

Lesson 1 The Path of a Billiard Ball

This lesson is one of my favorite activities! It brings back memories of when I created a simulation of this activity using Logo. I recall spending hours playing with different variations (shape of table, angle and starting position of ball) and trying to predict what would happen next. Looking back on this now, it would have been about 20 years ago, I would have been well advised to have paid closer attention to Jacobs first three lessons.

My approach was quite exciting, in large part because the computer did the actual graphing so I could quickly try different experiments. Jacobs' approach uses pencil and graph paper and is much slower and more tedious. But Jacobs acts like a mathematician whereas I acted like a boy enthralled with the technology. The difference is nicely captured by a brief article by Dave Pratt (Micromath Spring 1991, p. 28-9) where he described working with a class of children using Logo to draw fractal trees. "The idea was just as stimulating as I had hoped. The children produced some very impressive trees, and a forest developed on the classroom wall. ... So why did I feel uneasy? The children experimented freely but with little planning or control. They were becoming excited about the product, but I was becoming increasingly concerned about the thinking process. ... some of the best looking work was produced by children who had little understanding of the procedure itself."

This time I will try to act like a mathematician. It is not too late.

There are two issues to keep in mind while exploring the path of a billiard ball. One has to do with the variety of possible situations, and the other has to do with keeping track of what happens.

One might begin, as Jacobs does, by simply trying a few possibilities. He restricts himself to rectangular tables with integers for the lengths of the sides, and to only 45 degree paths and a starting position of the lower left corner. Even so, the variety of rectangular shapes makes a wide ranging different types of paths.

Underlying all of this is something critical. Curiosity. One must be intrigued by the situation. One needs to spontaneously generate questions. Jacobs tries to give a few examples. For the 8 different rectangles he provides, he asks: On which table does the ball have the simplest path? Can you explain why? What do you notice about the paths on tables 5 and 6? Can you explain? Do you think the ball will always end up in a corner? If the ball starts from the lower-left corner, do you think it can end up in any of the four corners?

Jacobs then goes on to comment on the complexity of the situation. He notes that the shape of a rectangular table depends on the width and the length and invokes a strategy that would be approved by both Piaget (formal operations stage) and Polya (think of a simpler problem). He keeps one variable constant and explores the effect of varying the other.

9:10 am I will continue with this later ...

6:30 am (2 days later) The first step is to find some paper and a pencil. I will scan these sheets later.

Here are the results of looking at tables with 1, 2 and 3 rows and enough columns to see the pattern.

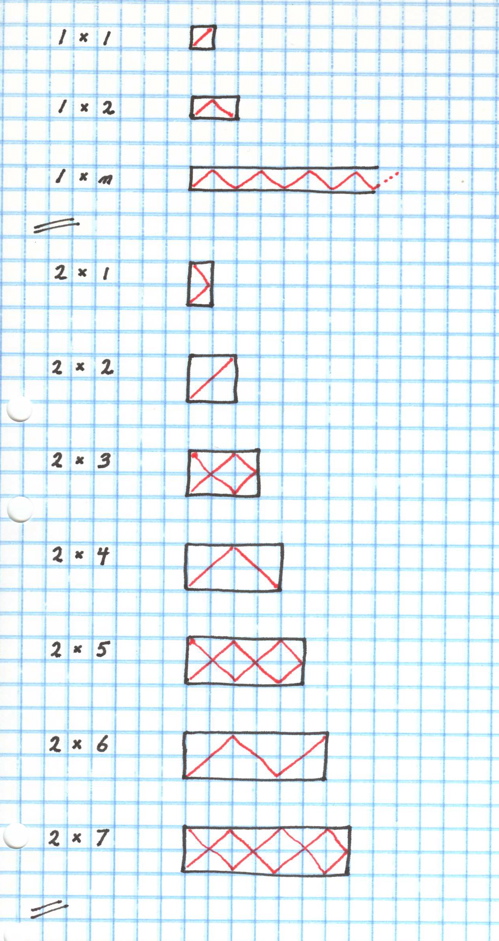
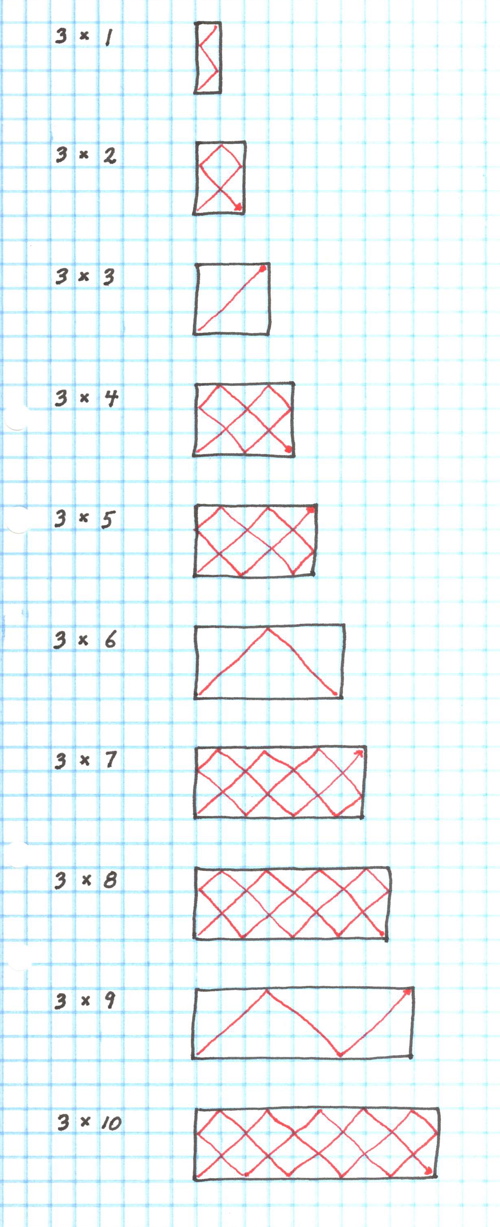
I have been careful to avoid looking at Jacobs. This is my activity. I am approaching it very systematically. I quit a particular set (i.e. with tables of 2 rows, or 3 rows) as soon as the pattern of the display becomes obvious. The number of distinct patterns appears to be dependent upon the number of rows in the table. When there are 2 rows the tables with an odd number of rows exhibit one pattern and the tables with an even number of rows exhibit a different pattern. When there are 3 rows the tables where the number of columns is a multiple of 3 exhibit one pattern, and tables where the number of columns is 1 more than a multiple of 3 exhibit a second pattern, and tables where the number of columns is 2 more than than a multiple of 3 exhibit a third pattern. This appears to be related to the idea of modulus. I am not yet confident of what will happen when I try looking at tables of 4 rows. I am wondering if there may be some repeating patterns (i.e. do tables with 2 and 4 rows have the same pattern?).

There are different ways of trying to summarize the results of these different situations. For example, where does the ball stop? (A ball only stops when it hits a corner). Let's try numbering the 4 corners 1, 2, 3, and 4 where 1 refers to the starting corner and then moving clockwise around the table.

Here are the stopping positions for a table with 1 row: 3, 4, 3, 4, 3, 4, 3, 4, ...

Here are the stopping positions for a table with 2 rows: 2, 3, 2, 4, 2, 3, 2, 4, 2, 3, 2, 4, ...

Here are the stopping positions for a table with 3 rows: 3, 4, 3, 4, 3, ...

I am impressed, and surprised, at how easily the pattern can be expressed by only looking at the end position.

Both by looking at the diagrams, and by looking at the sequence of numbers, one can (easily?) see that the ball never returns to the starting position. I am still uncertain about what happens when I move to a table with 4 rows.

Are there other ways of describing the pattern beside looking at the final position? Here are a couple of ideas that come to mind. Count the length of the path (in terms of the number of 'diagonal' lengths), count the number of times the ball touches a side of the table (this is equivalent to counting the number of times the ball changes direction), count the number of times the ball touches each side.

I am beginning to suspect that the different 'kinds' of patterns may be related to whether the number of rows is odd or even as well as if the number of columns is related to the modulus of the number of rows. I am also beginning to think that I may have to continue this experiment for at least the first dozen cases (i.e. when the number of rows is 1, 2, ... 12). This will take some time as I needed 10 tables to see the patterns for the case of only 3 rows. This brings to mind another feature of most school activities: they must be completed in a very short period of time. One example is to consider how many problems there are in a typical test and how long one has to complete it.

Let's press on and have a look at the 4 row case. 7:30 am

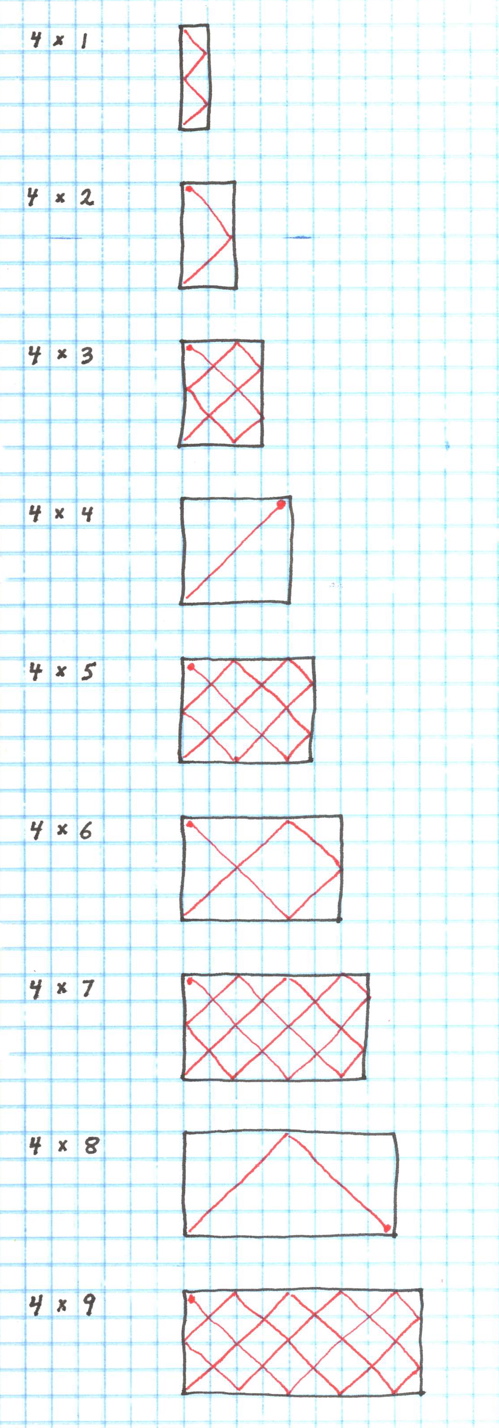
Fascinating. The tables with an odd number of columns cover all possible points, whereas when there are an even number of columns the path is much simpler.

Here are the stopping positions for a table with 4 rows: 2, 2, 2, 3, 2, 2, 2, 3, ...

I now want to work through the cases for 5, 6, 7, 8 and 9 rows. The even rows look like they will be similar to one another, but I am less confident of the odd rows. Both 5 and 7 are also prime numbers but 9 is composite. Will that make a difference? I think yes. The pattern will have some relationship to the number of factors of the rows and columns. This is becoming interesting.

So far I have restricted myself to integral values for the rows and columns and have always started in the same corner with a 45 degree angle. I think that many of the resulting patterns will have a relationship to modular arithmetic. But the situation can move from integral values to rational values, and to irrational values and one may be moving into calculus and the real number line. Instead of lines one might ask questions having to do with whether the path could cover all possible points on the surface of the table. One might also extend the table from 2 dimensions to 3 and play within various cubes. And why restrict oneself to quadrilaterals? What happens when one moves to pentagons, hexagons, ... Circular tables are the limiting case, as are spheres. But then there are hyperbolic surfaces.

This raises some, again for me, interesting questions having to do with the mathematics curriculum. Where does one find the balance between activities such as the above and activities that are not exploratory but which are aimed at either the development of skills or the deeper understanding that comes from considering the essential ideas underlying these activities? Perhaps a (very) crude first approximation could be 1/3, 1/3, 1/3. This assumes that one can accept the suggestion that there are three main types of mathematical knowledge: inductive exploration, deductive exploration and technical skills. This seems reasonable to me at the moment. But the critical point is that activities such as the above should be a critical core component of the mathematics curriculum at all grade levels, and this core component should occupy a significant proportion of the time allocated for mathematics. This is where one can have the actual experience of mathematics and the concomitant excitement that comes from playing with one's own ideas. This is currently missing in our present curriculum.