We explore direction fields (besides called slope fields) for some examples of first order differential equations.

Direction Fields for Outset Order Equations

We cannot (yet!) solve the differential equation However, from the equation solitary, we can deduce some facts about the solution. Recall that, geometrically speaking, the value of the first derivative of a function at a bespeak is the slope of the tangent line to the graph of the function at that point. And then, given a differential equation of the form

nosotros can interpret the value as the slope of the tangent line to the graph of at the point . Thus, the differential equation tells the states the slope of whatever solution passing through a given bespeak.

Consider the solution to the differential equation which passes through the point . What is the slope of the tangent line to solution at

By definition, a solution to this differential equation which passes through must have , and

Hence the slope is at .

The slope of at is .

Given a differential equation, say , we can choice points in the aeroplane and compute what the slope of a solution at those points will be. Repeating this process, we can generate a slope field. The slope field for the differential equation looks like this:

Permit'southward be explicit:

Here is the slope field for the differential equation , with a few solutions of the differential equation also graphed.

Each of the many solutions to the differential equation is adamant by initial conditions. The following interactive allows you to input the initial status in the dialog box. The output displays the slope field together with point and the solution that satisfies the initial condition.

Which of the five slope fields corresponds to the equation

Consider slopes of tangent lines in primal areas, such as the origin, each of the four quadrants. Are the tangent lines getting steeper as or increases?

Given a differential equation such as , information technology is piece of cake to find an explicit solution to the equation. (You lot may want to verify that functions of the class are solutions.) Notwithstanding, it's impossible to find explicit formulas for solutions of some differential equations. Even if in that location are such formulas, they may be then complicated that they're useless. In this case we may resort to graphical or numerical methods to go some thought of how the solutions of the given equation bear. Slope fields offering us one such method.

As we will see, the combination of direction fields and integral curves gives useful insights into the behavior of the solutions of the differential equation fifty-fifty if we can't obtain exact solutions.

We'll report numerical methods for solving a single first gild equation (eq:i.three.i) in Trench 3.ane - Trench 3.3. These methods can be used to plot solution curves of (eq:i.three.1) in a rectangular region if is continuous on . The figures in the three examples below evidence direction fields and solution curves for several differential equations of the class (eq:1.iii.i) with continuous for all .

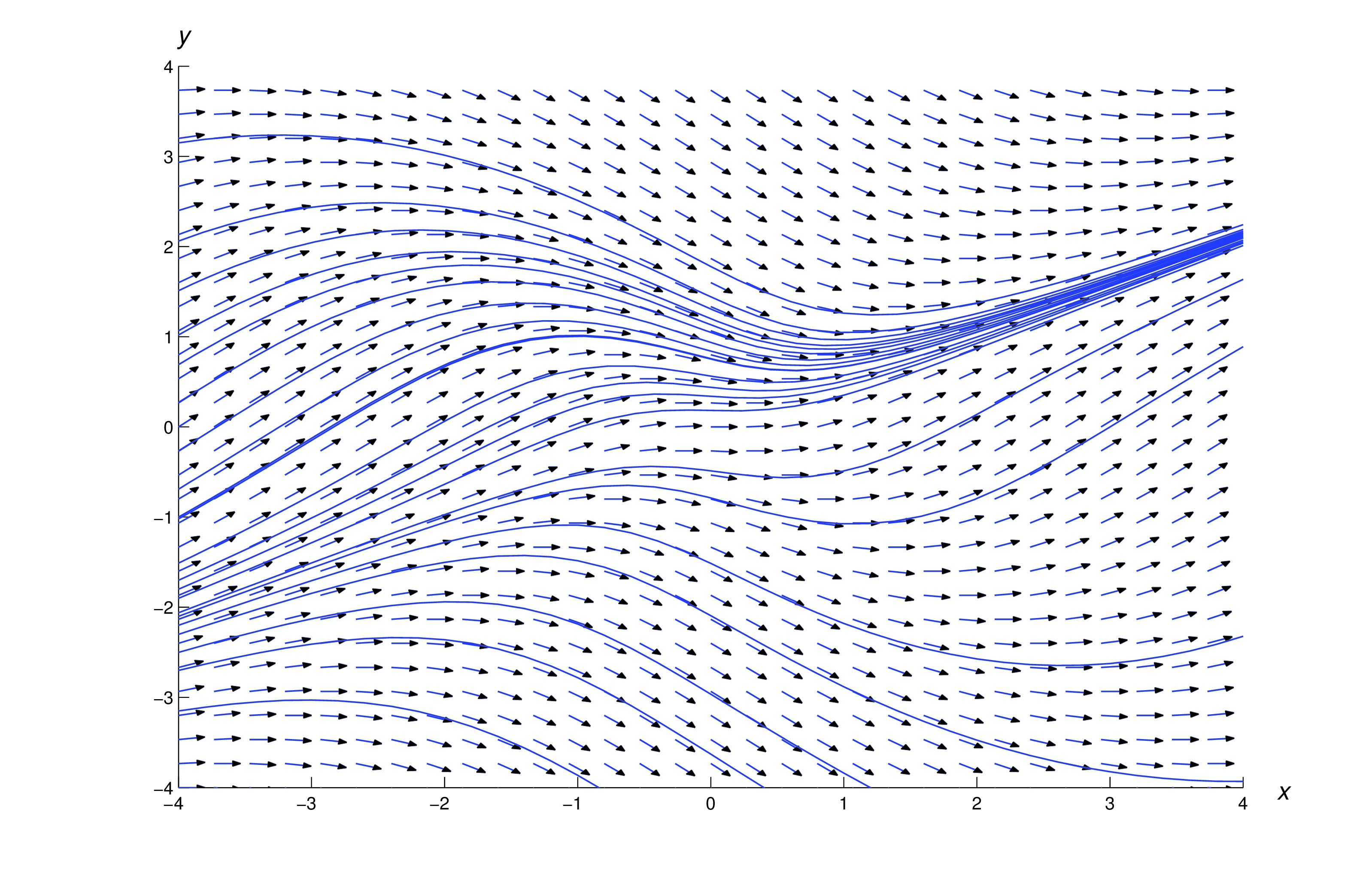
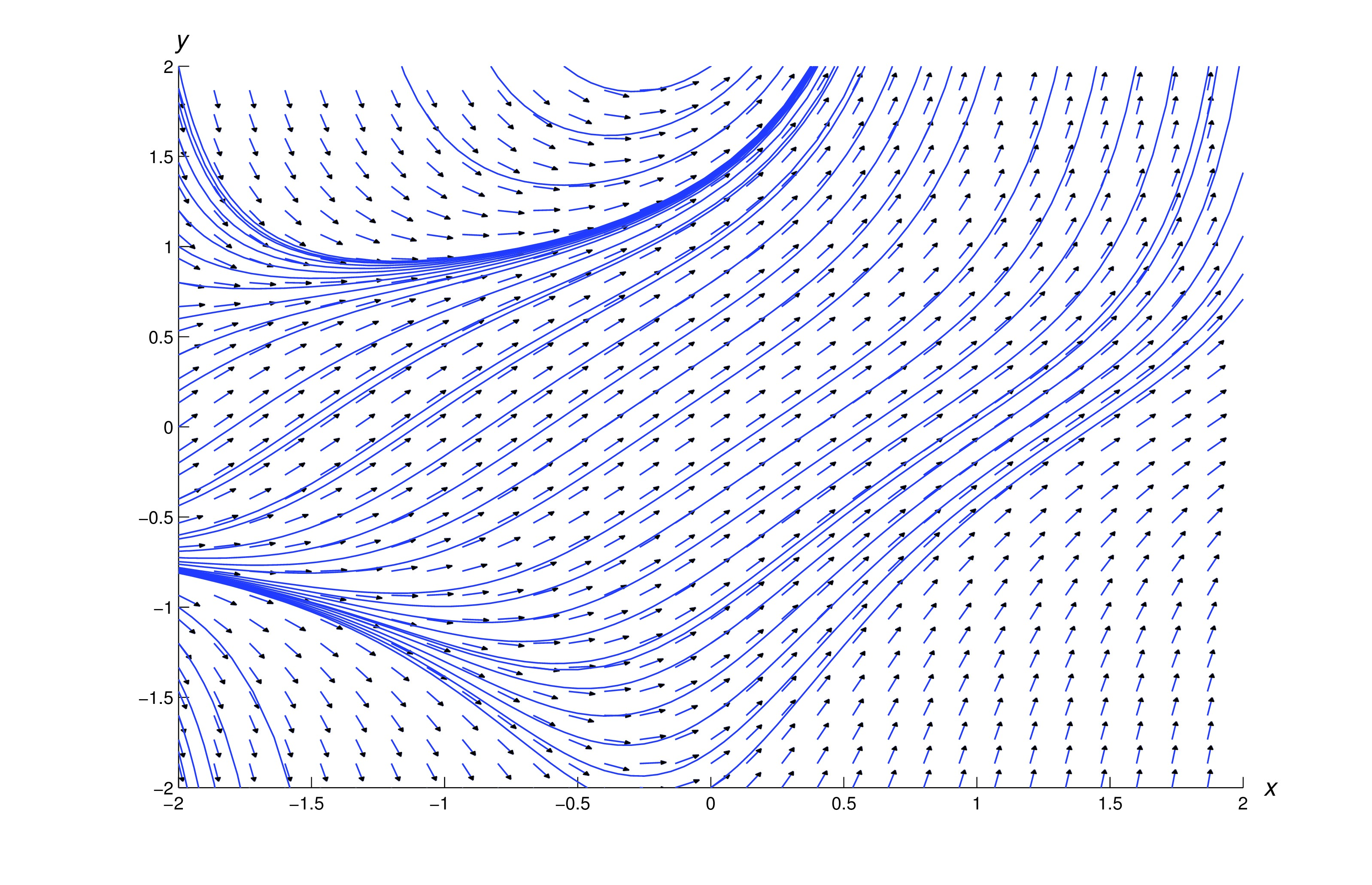
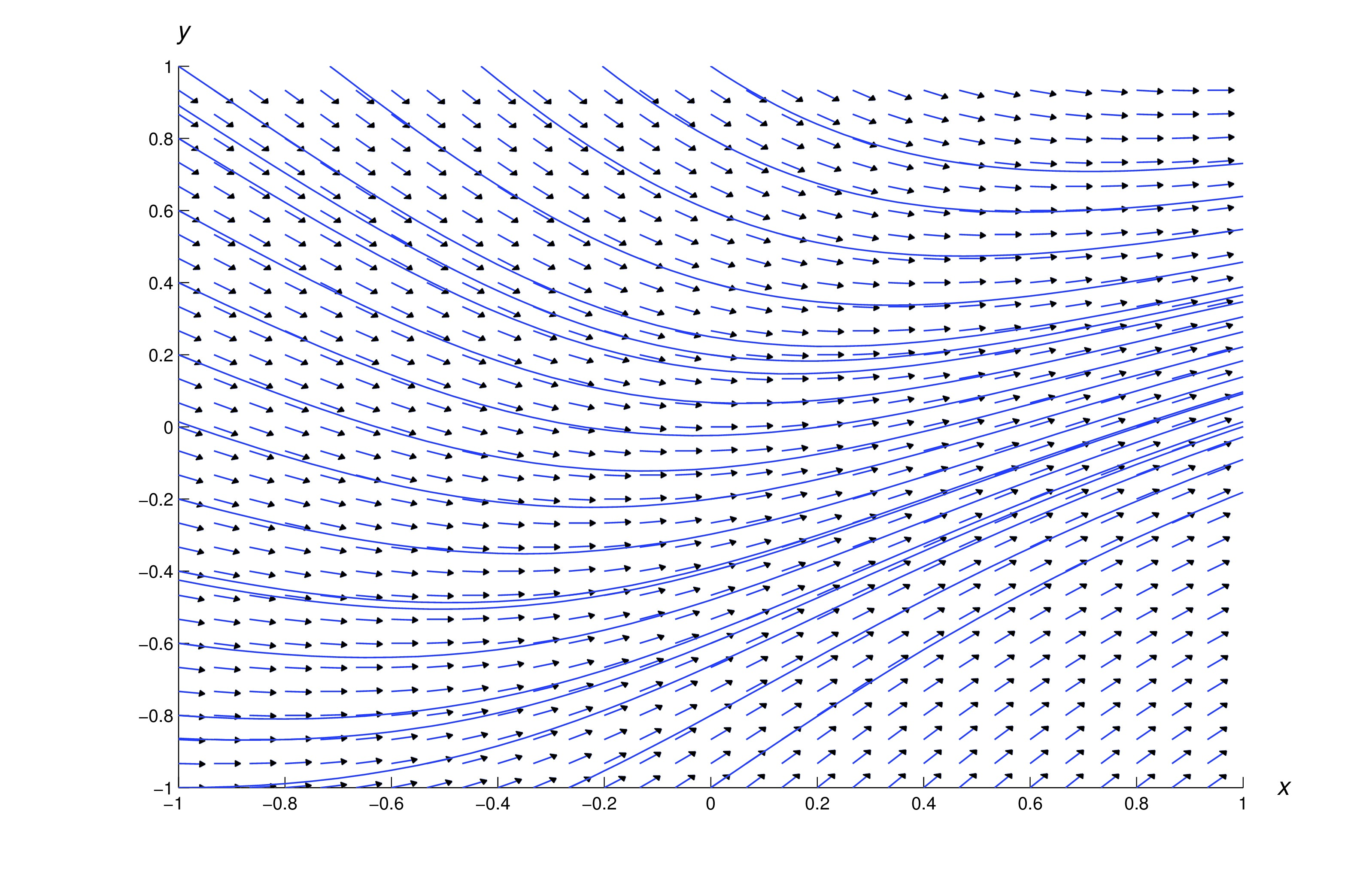
The methods of Trench iii.1 - Trench three.3 won't work for the equation if contains part of the -axis, since is undefined when . Similarly, they won't work for the equation if contains whatever part of the unit circumvolve , considering the correct side of (eq:1.iii.three) is undefined if . Nonetheless, (eq:ane.3.2) and (eq:one.3.3) can written equally where and are continuous on any rectangle . Because of this, some differential equation software is based on numerically solving pairs of equations of the form where and are regarded as functions of a parameter . If and satisfy these equations, and so so satisfies (eq:one.three.4).

Eqns. (eq:1.3.two) and (eq:one.iii.three) tin exist reformulated as in (eq:i.3.4) with and respectively.

The figure beneath shows a direction field and some integral curves for . Equally we saw in Example example:1.2.1, the integral curves of (eq:1.3.two) are circles centered at the origin.

PIC

The effigy below shows a management field and some integral curves for .

PIC

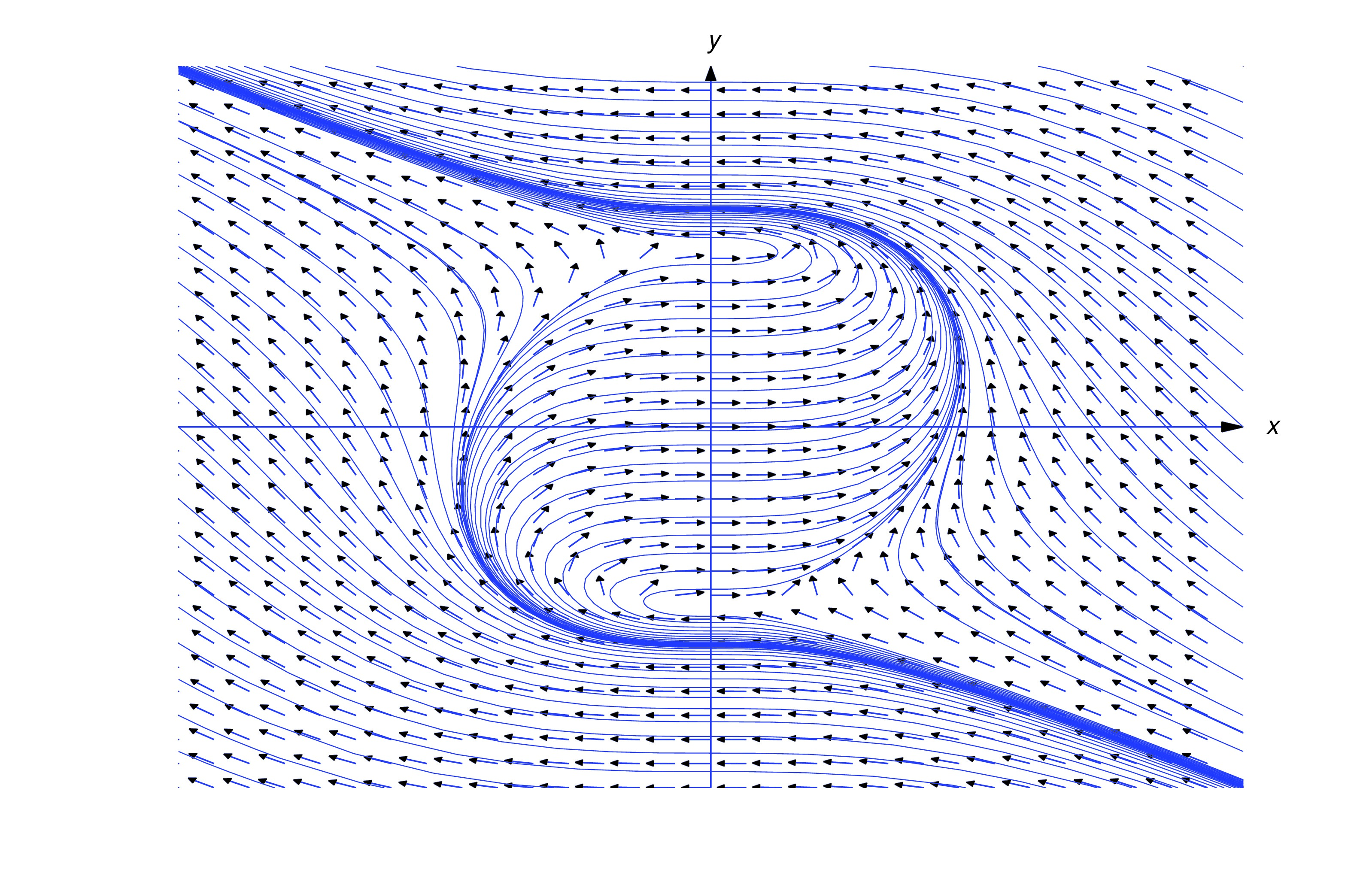
The integral curves near the top and lesser are solution curves. All the same, the integral curves near the heart are more than complicated. For case, the effigy beneath shows the integral bend through the origin. The vertices of the dashed rectangle are on the circle (, ), where all integral curves of (eq:1.3.3) have infinite slope.

PIC

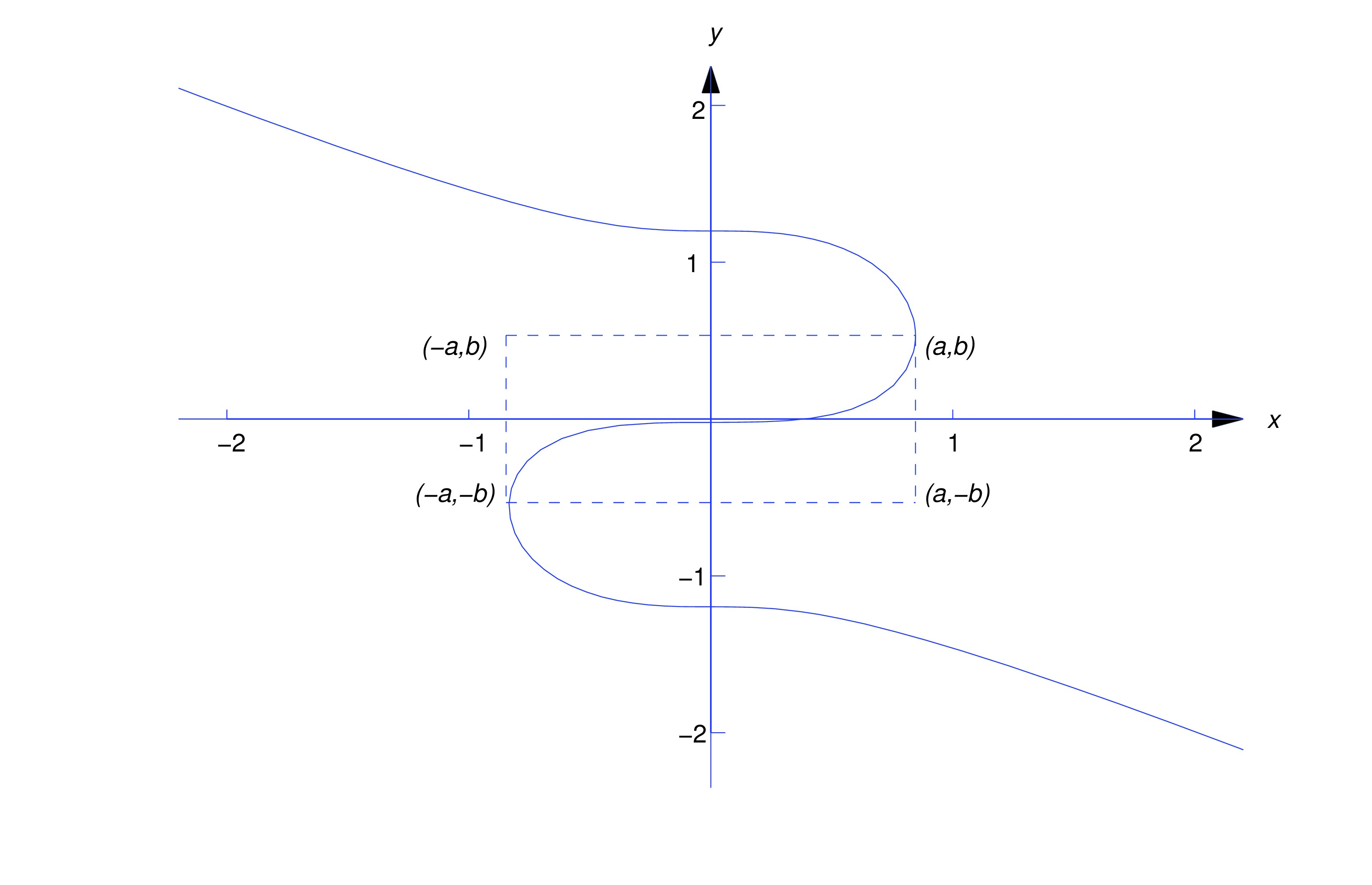
There are three solution curves of (eq:1.three.3) on the integral bend in the figure: the segment in a higher place the level is the graph of a solution on , the segment below the level is the graph of a solution on , and the segment between these ii levels is the graph of a solution on .

Even if is continuous and otherwise "nice" throughout , your software may require you to reformulate the equation as which is of the form (eq:1.3.5) with and .

As you study from this book, you'll ofttimes be asked to use computer software and graphics. Often you lot may not completely understand how the software does what it does. This is like to the situation most people are in when they bulldoze automobiles or scout television, and it doesn't decrease the value of using modern technology as an aid to learning. Just be careful that yous use the technology every bit a supplement to idea rather than a substitute for information technology.

Text Source

MOOCulus, Numerical Methods (CC-BY-NC-SA)

Trench, William F., "Elementary Differential Equations" (2013). Faculty Authored and Edited Books & CDs. viii. (CC-Past-NC-SA)

https://digitalcommons.trinity.edu/mono/viii/